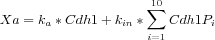COPASI: Projects/Multistate Model Builder/First multistate model

Building the first multistate model

In this section we describe step-by-step how to build a simple multistate model filling the different tables of MSMB.

As a running example, we use a small model at the core of the budding yeast cell cycle process. The small model presented in this section contains all the main components of a classical multistate problem and it describes the antagonistic relationship between ClbM and Cdh1 proteins (we refer the reader to the original publication [Barik2010] for the complete characterization of the model).

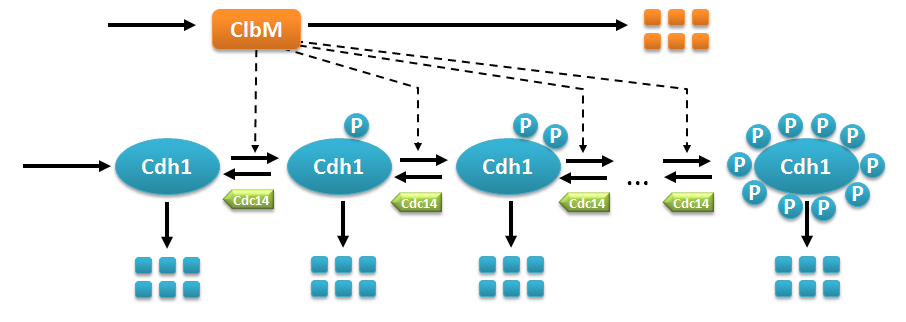Multistate reaction at the core of a budding yeast cell cycle model. The figure shows the core reactions of the model. We have a total of eleven forms (or states) of Cdh1: a non-phosphorylated form (Cdh1) and ten phosphorylated forms denoted as

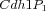
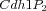
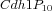
$Cdh1P_{1}$ , $Cdh1P_{2}$ , ..., $Cdh1P_{10}$ .

Some of these forms take part in specific phosphorylation and dephosphorylation reactions as reactant or product: intuitively every form with i phosphate groups has a successor form i+1 and a predecessor form i-1. So, even if the intuitive description of this model include just the "reactions" successor/predecessor (plus the two cases of i=0, which has no predecessor, and i=10, which has no successor), the classical way of modelling this system is to explicitly write the total of 34 single state reactions in the Table below. All those reactions are necessary because each phosphorylation state is considered as a distinct species.

To complete the description of this small model we have also to consider the fact that all eleven forms of Cdh1 take part in the degradation of ClbM.

	Reaction	Equation
1	`->` ClbM	ks
2	ClbM `->`	ClbM ⋅ Xa
3	ClbM + Cdh1 `->` ClbM + Cdh1P₁	kp ⋅ ClbM ⋅ Cdh1
4	ClbM + Cdh1P₁ `->` ClbM + Cdh1P₂	kp ⋅ ClbM ⋅ Cdh1P₁
5	ClbM + Cdh1P₂ `->` ClbM + Cdh1P₃	kp ⋅ ClbM ⋅ Cdh1P₂
6	ClbM + Cdh1P₃ `->` ClbM + Cdh1P₄	kp ⋅ ClbM ⋅ Cdh1P₃
7	ClbM + Cdh1P₄ `->` ClbM + Cdh1P₅	kp ⋅ ClbM ⋅ Cdh1P₄
8	ClbM + Cdh1P₅ `->` ClbM + Cdh1P₆	kp ⋅ ClbM ⋅ Cdh1P₅
9	ClbM + Cdh1P₆ `->` ClbM + Cdh1P₇	kp ⋅ ClbM ⋅ Cdh1P₆
10	ClbM + Cdh1P₇ `->` ClbM + Cdh1P₈	kp ⋅ ClbM ⋅ Cdh1P₇
11	ClbM + Cdh1P₈ `->` ClbM + Cdh1P₉	kp ⋅ ClbM ⋅ Cdh1P₈
12	ClbM + Cdh1P₉ `->` ClbM + Cdh1P₁₀	kp ⋅ ClbM ⋅ Cdh1P₉
13	Cdc14 + Cdh1P₁ `->` Cdc14 + Cdh1	kh ⋅ Cdc14 ⋅ Cdh1P₁
14	Cdc14 + Cdh1P₂ `->` Cdc14 + Cdh1P₁	kh ⋅ Cdc14 ⋅ Cdh1P₂
15	Cdc14 + Cdh1P₃ `->` Cdc14 + Cdh1P₂	kh ⋅ Cdc14 ⋅ Cdh1P₃
16	Cdc14 + Cdh1P₄ `->` Cdc14 + Cdh1P₃	kh ⋅ Cdc14 ⋅ Cdh1P₄
17	Cdc14 + Cdh1P₅ `->` Cdc14 + Cdh1P₄	kh ⋅ Cdc14 ⋅ Cdh1P₅
18	Cdc14 + Cdh1P₆ `->` Cdc14 + Cdh1P₅	kh ⋅ Cdc14 ⋅ Cdh1P₆
19	Cdc14 + Cdh1P₇ `->` Cdc14 + Cdh1P₆	kh ⋅ Cdc14 ⋅ Cdh1P₇
20	Cdc14 + Cdh1P₈ `->` Cdc14 + Cdh1P₇	kh ⋅ Cdc14 ⋅ Cdh1P₈
21	Cdc14 + Cdh1P₉ `->` Cdc14 + Cdh1P₈	kh ⋅ Cdc14 ⋅ Cdh1P₉
22	Cdc14 + Cdh1P₁₀ `->` Cdc14 + Cdh1P₉	kh ⋅ Cdc14 ⋅ Cdh1P₁₀
23	Cdh1 `->`	kd ⋅ Cdh1
24	Cdh1P₁ `->`	kd ⋅ Cdh1P₁
25	Cdh1P₂ `->`	kd ⋅ Cdh1P₂
26	Cdh1P₃ `->`	kd ⋅ Cdh1P₃
27	Cdh1P₄ `->`	kd ⋅ Cdh1P₄
28	Cdh1P₅ `->`	kd ⋅ Cdh1P₅
29	Cdh1P₆ `->`	kd ⋅ Cdh1P₆
30	Cdh1P₇ `->`	kd ⋅ Cdh1P₇
31	Cdh1P₈ `->`	kd ⋅ Cdh1P₈
32	Cdh1P₉ `->`	kd ⋅ Cdh1P₉
33	Cdh1P₁₀ `->`	kd ⋅ Cdh1P₁₀
34	`->` Cdh1	ks1

List of reaction needed to encode the model described above.
As we can see from the table above, most of the reactions has the same general structure (and rate law) so what the modeller would actually want to have is a way to define Cdh1 states with a range of ordered indexes and a way to refer to the successive/preceding state.

In this case, we have the following definition of Cdh1:

Cdh1(p{0:10})

The intuition behind the definition is that the species called Cdh1 has a site (called p) which can have different state values, and those state values ranges from 0 to 10 (as integer numbers). For a detailed description of the syntax of multistate species and reactions, we refer the reader to Section Multistate Species and Reactions syntax.

We can use this compact notation, to reduce the number of reactions from the initial 34 down to 5, by expressing the reactants and products as multistate species.

	Reaction	Equation
1	`->` ClbM	ks
2	ClbM `->`	ClbM ⋅ Xa
3	ClbM + Cdh1(p{0:9}) `->` ClbM + Cdh1(succ(p))	kp ⋅ ClbM ⋅ Cdh1(p)
4	Cdc14 + Cdh1(p{1:10}) `->` Cdc14 + Cdh1(pred(p))	kh ⋅ Cdc14 ⋅ Cdh1(p)
5	Cdh1(p{0:10}) `->`	kd ⋅ Cdh1(p)
6	`->` Cdh1(p{0})	ks1

In Reaction 2, Xa is the activity of Cdh1 expressed as the weighted sum of its phosphorylated and unphosphorylated forms.

In particular we have that

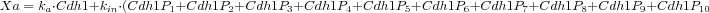
$Xa = k_a \cdot Cdh1 + k_{in} \cdot(&Cdh1P_1 + Cdh1P_2 +Cdh1P_3+Cdh1P_4 + Cdh1P_5 +Cdh1P_6+Cdh1P_7+Cdh1P_8+Cdh1P_9+Cdh1P_{10}$ )

What the user needs is, again, a compact way to represent this sort of expressions taking advantage of the multistate format and a summation operator as follows:

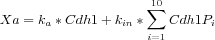
$Xa = k_a * Cdh1 + k_{in}*\sum_{i=1}^{10} Cdh1P_i$

In MSMB it is possible to define the above summation in a compact way as follows:

ka * Cdh1(p{0}) + kin * SUM(Cdh1;p{1:10})

This summation operator make the expression easy to view, manipulate and edit.

As today, there are no tools which support the multistate format directly.
Even SBML does not provide a direct way to express multistate species and reactions.
Therefore MSMB provides support to expand the compact (multistate) model into a single-state species model that can be used with any other SBML-compliant tools for simulation and further analysis.

The importance of the multistate concept is, however, acknowledged by the SBML community and there is an ongoing effort in defining a multi package for the SBML Level 3 specification (Multistate and Multicomponent Species (multi)). The multi package whose purpose is to define "object structures for representing entity pools with multiple states and composed of multiple components, and reaction rules involving them". The package is still in the proposal stage, but we are going to offer direct export to the sbml-multi format, once the specification reaches the final approved stage.

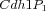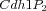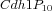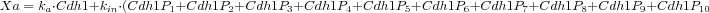First Multistate Model

Building the first multistate model